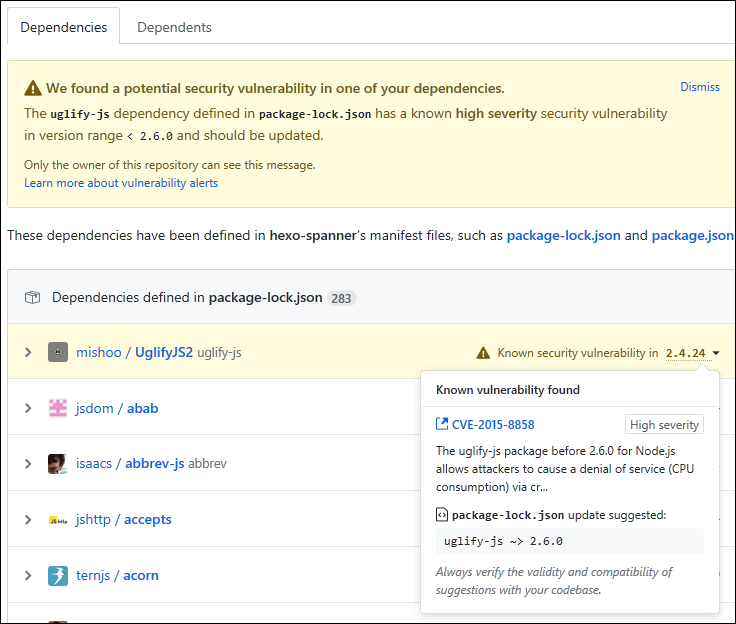
2019-11-06 Update: This blog is obsolete and no longer being maintained here. These Miser Project Posts are now maintained and continued at Orcmid’s Lair, the reboot. The authoritative version of this page is now at
https://orcmid.blogspot.com/2019/02/miser-project-interpretation.html
“When a Mathematical Reasoning can be had it’s as great a folly to make use of any other, as to grope for a thing in the dark, when you have a Candle standing by you.”
— John Arbuthnot, Of the Laws of Chance, 1692.
Miser Project conception starts from reasoning with and in certain mathematical structures. That foundation applies mathematical thinking in establishing a model of computation and subsequent reasoning about programs and their dependable employment for practical purposes. It is not necessary to digest all of the mathematics in order to develop and use the eventual software. It is expected that provided there is trustworthy assurance of suitable quality, an objective of the mathematical route: someone has done it checked the math and verified the software in a transparent and trustworthy undertaking. and that undertaking is transparent and trustworthy.
I strongly recommend the wider and practical context presented in Edward Ashford Lee’s recent book, Plato and the Nerd. For the Miser Project, “theory” and “context” are often used in place of Lee’s use of “model” and “paradigm.” The Miser Project use of “model” is reserved for a mathematical- logic situation around interpretations of theories, a flavor of modeling (or theory-building) that exposes the marvelous utility of computers as instruments of human purpose and experience that Lee addresses. The notion of ontological commitment is put forth as an informal alternative to paradigm when stepping into a particular perspective is undertaken intentionally and with self-awareness of the manifest context.
The Eugenia Cheng book, The Art of Logic: How to Make Sense in a World that Doesn’t looks critically into affairs of the world from a mathematician’s perspective. More profound than the narrow application of mathematics in the Miser Project conception of computing, Cheng’s video on “How to Think Like a Mathematician” reveals some connections with the structures portrayed in boole.txt and the as representations and interpretations related to ‹ob›.
In the course of the Miser Project and demonstration of computational power and limitations, some specialized concepts are depended on appealed to. They are elaborated here in this post.
2019-11-04 Penultimate Draft: Some major adjustments and stitching in notions of ontological commitment prior to digging into the ‹ob› computational model direction.
2019-04-02 Intermediate Refinements: Additional diagrams and adjustments to smooth the narrative, reflecting suggestions by colleague William L. Anderson.
2019-02-11 Initial Public Draft: Lengthy article navigating some concepts that will arise continuously in narration of the computational model and its representation in computational processes. For reference and review as background to further articles.
Preliminaries
Content
- Recap: Computation-Model Stage-Setting
- Structure, Interpretation, Representation, Computation, and Manifestation
- Review: More About Structure
- Concerning Representational Ambiguity
- Choreography of Computation
- Manifestation and Tacit Awareness
- Ontological Commitment: Layered Abstraction
1. Recap: Computation-Model Stage-Setting
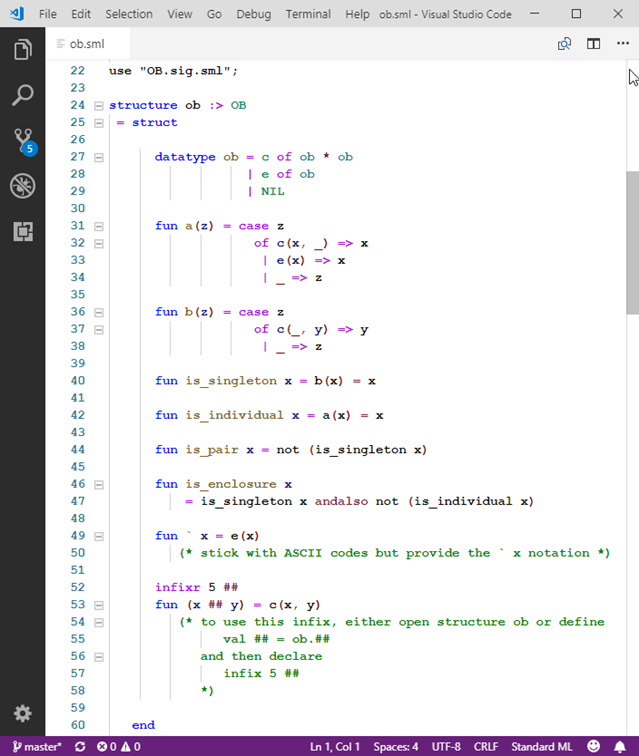
We have not escaped from mathematical entities so far in this series of articles, apart from one programming-language mock-up of an ‹ob› computational interpretation.
At this point, these articles address ‹ob› = 〈Ob,Of,Ot〉having a domain of discourse, Ob, that is a flavor of abstract data structure, strictly on theoretical terms. With regard to computational interpretation, effective-computability is then taken as a condition on deductions that are available given a particular mathematical representation of a function or predicate. The transition from an effectively-computable representation in any structure to an operational computational process of any kind is suggested, with interpretation in ‹ob› as the path to demonstration.
Interpretation of other structures and their effectively-computable primitives via representations in ‹ob› sets the stage for valid computational interpretation satisfying in the ‹ob› computational model. That is, if we are satisfied about the ‹ob› computational model, then we have an indirect means for enactment of computations with respect to other structures that are successfully interpreted in ‹ob›. Such transition from other/higher levels to ones tied to the lower-level computational model demonstrates applicability of computational interpretation.
It is posited that the interpretation-in-‹ob› approach is sufficient for computational representation of the same effectively-calculable mathematical functions as any other recognized model of computation. Demonstration of such universality (i.e., Church-Turing computability) and common limitations of that universality is one Miser Project objective: making this aspect of theoretical computing accessible in practical, demonstrable, and understandable terms for computing practitioners and other interested parties.
The ‹ob› model of computation, although very simple, is a sufficient foundation for computational-interpretation by stored-program operations that manifest layers of abstraction. By stored-program is meant taking obs themselves as scripts for operations on obs taken as operands. Such scripts can direct derivation of obs to be taken as further scripts, illustrating how computer programs (e.g., compilers) are used to generate (compile) further computer programs from descriptions in their data (e.g., programming-language texts), extending the practical reach of computer applications.
Narration of the ‹ob› model of computation is the subject of the next series of blog articles. The model is founded on two function representations: one by obap.ap(p, x) and one by obap.eval(e). The operands, p, x, and e, are obs. Given definite obs for operands, any determined result is a definite ob.
Dependable manifestation of the computational model in implemented operations of a physical digital computer rests on empirical determination that the computer’s performance yields valid computation-model interpretations. All of that will be explored.
2. Structure, Interpretation, Representation, Computation, Manifestation, and Ontological Commitment
Some informal notions are adapted and restricted in the context of the Miser Project. These specialized concepts assist in capturing the essence of computation and its practical application. This framing is not the only perspective. It is offered as one useful way to appreciate computation by digital computer procedures. Briefly, in rough progression.
- Structure
mathematical characterization of theoretical entities in terms of domains, primitive notions, and applied logical theories
- Interpretation
- mathematical: arrangements by which one mathematical structure is modelled in another using a mathematically-demonstrated correspondence
- linguistical: interpretation of a text in a (standard) semantic domain, including computation-model interpretation of programming-language texts
- empirical: engineering of mechanized operations confirmed to satisfy a model of computation; realized computational interpretation
- social/scientific: identifying objects in physical/social reality as evocative of theoretical entities, and sometimes vice versa; taking such determinations as pertaining to relationships in contingent reality
- typically, standing in some structure and projecting its fundamental entities on some other theoretical structure or experience of nature that satisfies the original in some (contingent) manner.
- Representation
- mathematical: formulation of mathematical functions in a given structure’s theory language, effectively determining the nature of the functions as theoretical entities; notionally, mathematically-equivalent formulations
of the same functioncan be taken ashaving the same functional interpretationrepresenting the same function. - conceptual: the entities and functions of one structure that serve as interpretations (representatives) for those of another, thereby representing that other structure; ideally, the represented
individualsentities are readily discerned upon inspection of (computationally) derivedrepresentationsrepresentatives.(presentations are traceable back to the intended interpreted entities in a particular context) reflectivetypically: a representation may provide multipleentitiesrepresentativesthat are equivalent as valid interpretations of a singleof the same entity in another structure; in general, representatives are not exclusive to some particular representation, context being required to ascertain the entity the representative is an intended interpretation for (e.g., thepropositional algebra simulation by ob.p01.bp in contrast with the subsumed ob.NE.bp interpretationmany ways that every single ob is representative in interpretations of Boolean Algebra elementsob of ‹bp›as in boole.txt).
- Computation
- conceptual: performance of (algorithmic) procedure p such that representation of some entity x, the operand/data, is transformed into a representation of y,
- informal: the result of a computation, spoken of as the represented entity (e.g., “the square-root of x”, “the estimated fastest route from city A to city B today”, or, “interactive achievement of the end-game in Tomb Raider”)
- Manifestation
- general: perceptual object of attention recognized
inas evocative (manifesting) some other object or activity - operational: act of producing/presenting objects or activities taken
asto be so evocative - interactive: with computer systems, the appearance evoked in the representation of computational results/operation on some medium (e.g., the perceived images on the surface of a computer-operated graphical display)
- tacit: objects perceived as being manipulated via interaction with a computer system operating in keeping with manifestation fidelity, (e.g., the conceptual document simulated via word-processing software)
- Ontological Commitment
- linguistical: speaking of (theoretical/conceptual/notional) abstract entities as if they exist apart from manifestation in language (e.g., unicorns, numbers, the obs of the mathematical structure ‹ob›)
- pragmatic: granting being to manifest entities (what a manifestation is said to be of) and the means of manifestation (what the manifestation is without considering it as a representation), while avoiding category error: confusion of the entity manifest with a manifestation of it, notwithstanding the practical fidelity by which the manifestation is sustained
- tacit: granting existence to non-perceivable entities that arise exclusively in language — can only be talked about — whatever the agreement and behavior concerning their reality; such commitments can constrain/oppose others.
3. Review: More About Structure
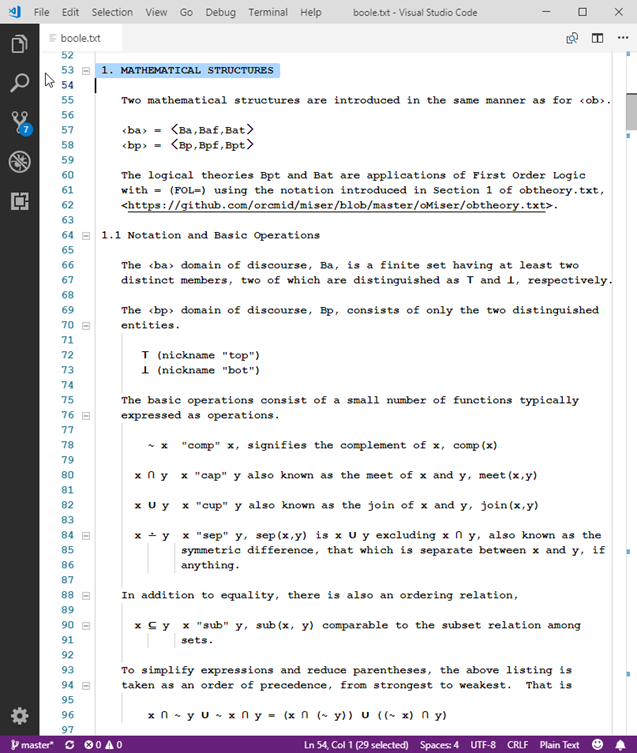
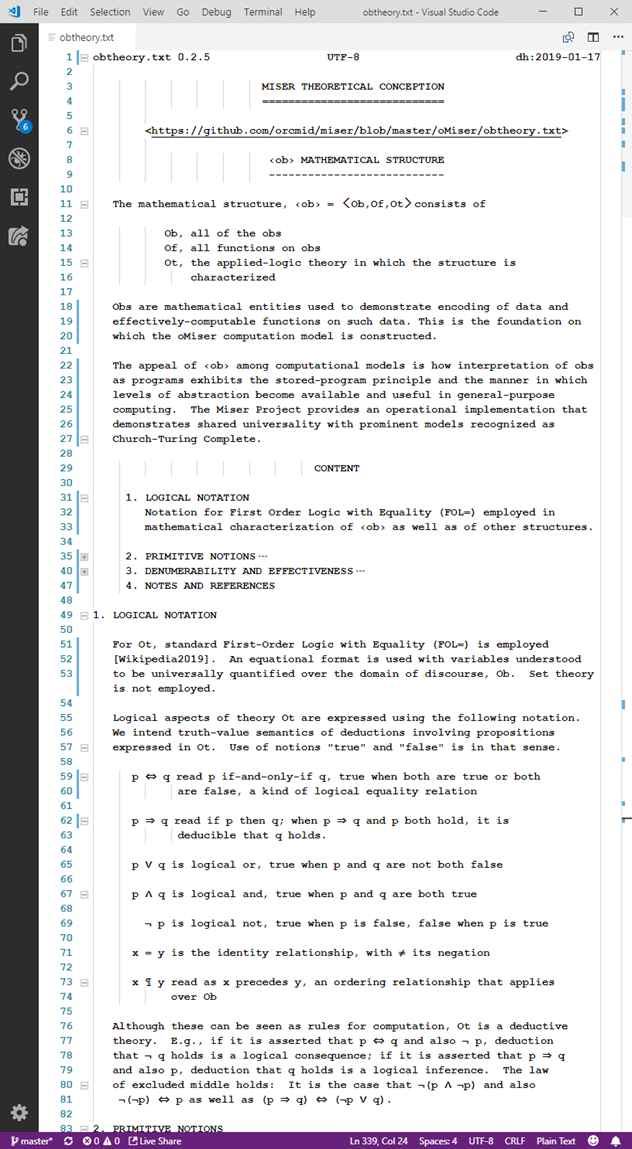
Expositions of mathematical structures such as ‹ob› = 〈Ob,Of,Ot〉circumscribe particular theoretical entities in a mathematical-logic framework. The general pattern is ‹s› = 〈Sd,Sf,St〉.
- Sd signify the domain of discourse, the collection of entities all of a single kind that are the subject of variables, such as x, y, z, in expressions of the structure (with universal quantification, such as with ∀x∀y∀z, usually implicit)
- Sf signify all of the functions and predicates with operands and function yields in Sd. Individual functions become know by their representation using St.
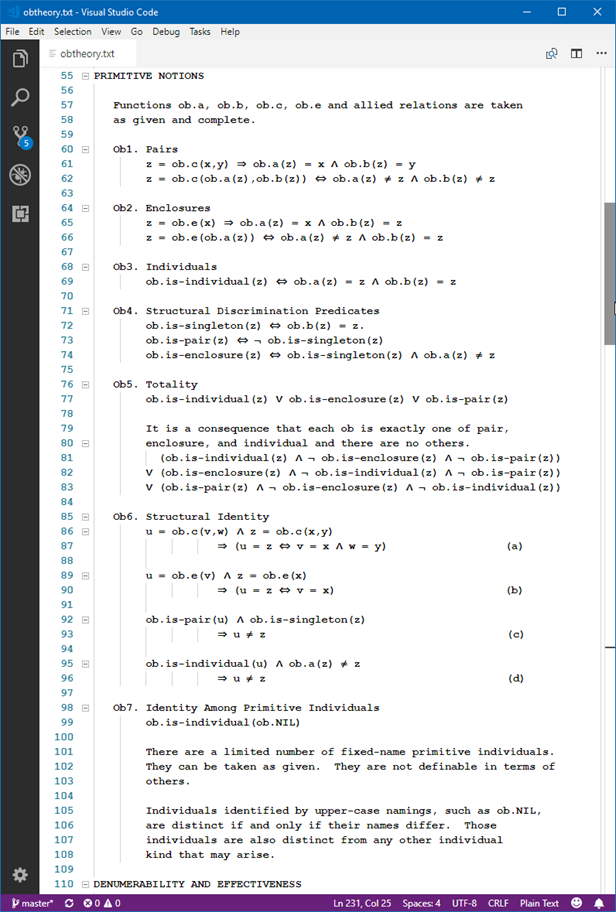
- St consist of the expressions that establish primitive notions, axioms, and function representations using a mathematical system of logic. The subject matter is always Sd and explicitly-represented elements of Sf. Certain functions and predicates may be taken as axiomatic, with all others expressible in terms of those.
For the Miser Project, St is typically an application of First-Order Logic, usually with = (FOL=). This is the case of ‹ob›.
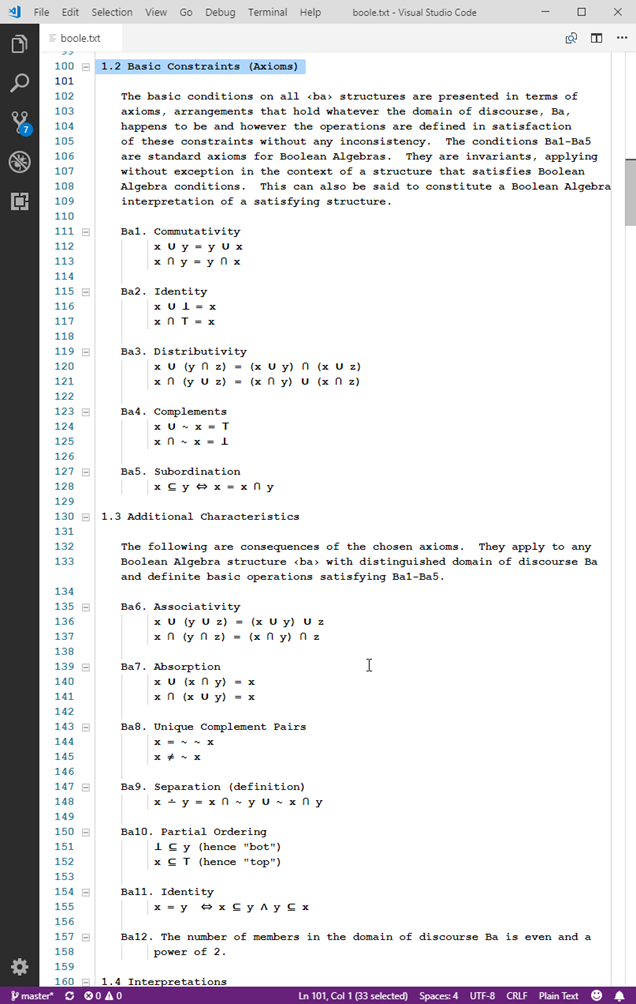
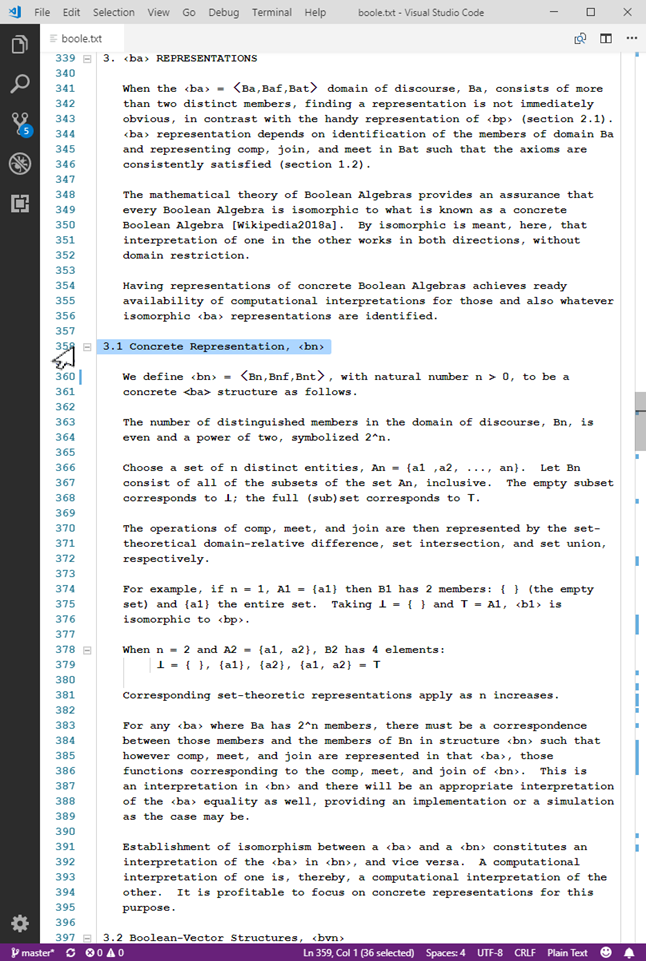
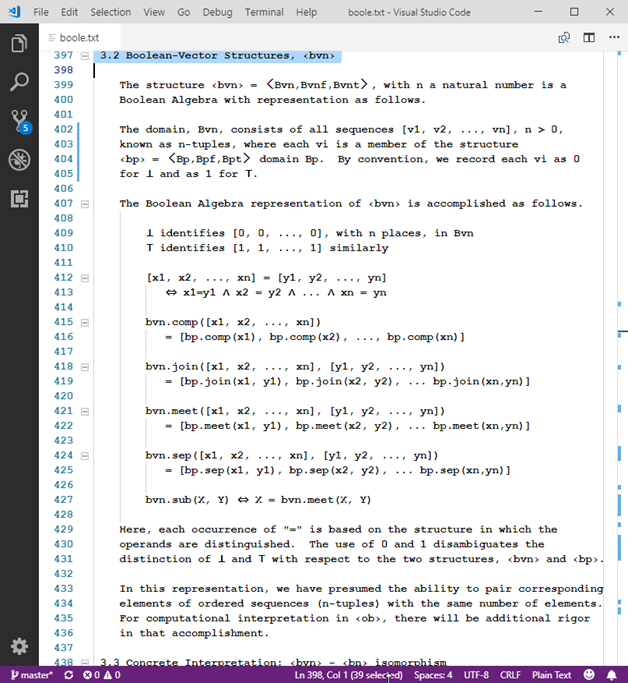
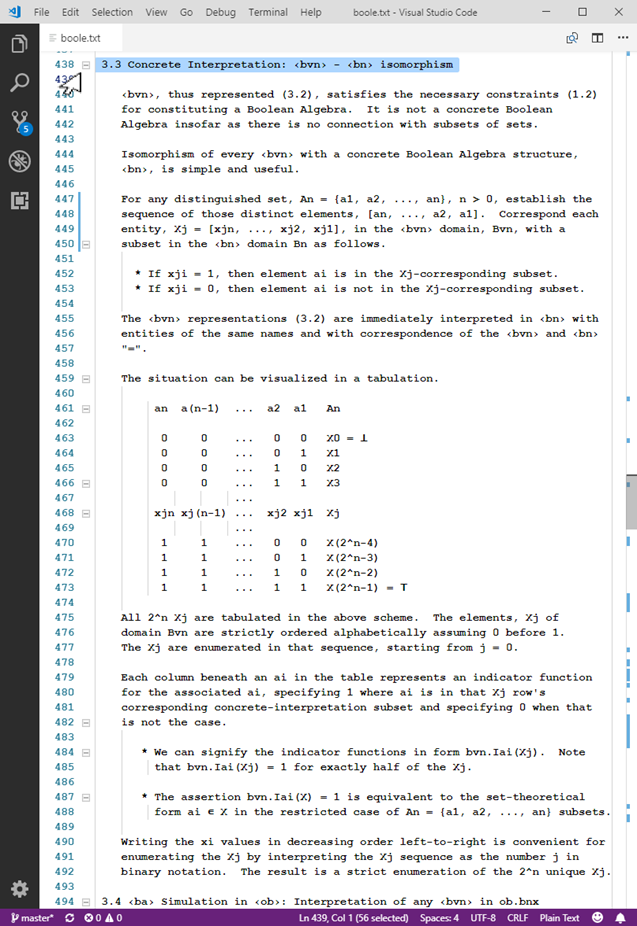
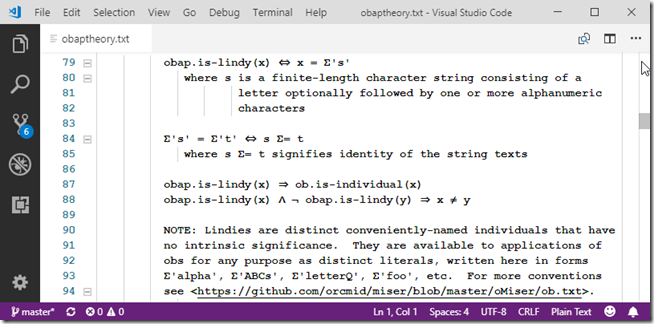
Distinguishing mathematical structures in this manner allows examination of multiple structures and connections among them. To be explicit about a structure being appealed to in a given discussion, prefixed names such as ob.c, ob.NIL, bp.top, bvn.comp, and ob.bvx.cf provide clarity in identifying the “host” structure, entities of that structure’s domain, and the entities being interpreted as particular representations there, and the specific means of representation. So far, in addition to ‹ob›, the Boolean Algebra structure ‹ba› and its kin ‹bp›, ‹bn›, and ‹bvn› have been explored along with various representations in each other and in ‹ob›. The curious representation, ob.bvx, of any Boolean Algebra on a denumerable domain will invite further attention in the computational interpretation of number theory.
Structures evoke theoretical entities. There is no inherent suggestion of material or natural existence. Rather, the Sd and Sf arise entirely in language St and live entirely in mathematics, so to speak. Whatever conceptual notions one might harbor about the subject of a structure, consideration and discussion of the properties of such entities is confined to what can be reconciled entirely via expression and deduction in applied-logic theory St, along with any informal statements (meta-conditions) that restrict/inform the constructions and valid deductions. There is no necessity of ontological commitment to such theoretical entities, although it creeps into our speaking of them nonetheless; it is a matter of linguistical economy.
4. Interpretation: Variations on a Theme
Matters of interpretation arise in varied forms with respect to the Miser Project.
Mathematically, “interpretation” is used with regard to a correspondence between one structure, ‹A›, and another, ‹B›. Typically, there are four parts:
- Match each element of ‹A›’s domain of discourse with a distinct member of ‹B›’s domain. Given x in ‹A›, signify its interpretation in ‹B› by Ix.
- Represent functions and predicates in ‹B› that are interpreted as representations of corresponding
identified as corresponding interpretations of theprimitives of ‹A›. - If the theory of ‹A› is an application of FOL=, represent
interpret“x = y” of ‹A› with ‹B› predicate b.I.a.is-eq(Ix, Iy), or simply Ix =I Iy.
When
b.I.a.is-eq(Ix, Iy) ⇔ Ix = Iy
in Bt of ‹B›, the interpretation is said to be an implementation of ‹A› in ‹B›; otherwise, it is said to be a simulation of ‹A› in ‹B›. The use of I (in bold or script) is made specific in terms of ‹B› representations when it is necessary to distinguish among multiple interpretations of ‹A› in ‹B› - The interpretation is valid when all deductions in structure ‹A› are mirrored by deduction of the corresponding interpretation in structure ‹B›.
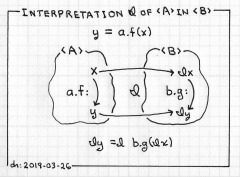 Valid interpretation of ‹A› in ‹B› need not capture all features and entities of ‹B›. Validity achievement only signifies successful interpretation of ‹A›.
Valid interpretation of ‹A› in ‹B› need not capture all features and entities of ‹B›. Validity achievement only signifies successful interpretation of ‹A›.
An intended interpretation of a structure might be invalid. In that case, the offered interpretation may be defective or the structures ‹A› and/or ‹B› ill-suited to the intended purpose. Resolution of the matter is external (meta) to the structures themselves.
The diagrammatic use of arrows, above, is suggestive of constructions in mathematical category theory. That is inessential here; informal use of interpretation, including for non-mathematical purposes, is sufficient for computation-model formulation. Consideration of rigorous category-theoretical approaches is deferred.
Texts or other concrete forms of expression satisfying a formal grammar can have specified interpretations as entities in a structure having computational interpretation. That form of interpretation will be demonstrated with the parsing of expressions that are interpreted in terms of some construction, such as ‹ob› computation-model operations.
Interpretations are also made between entities of mathematical structures and domains of non-mathematical character, such as observations in nature, predictions of scientific theories, and many practical and artistic situations. Acceptability is an empirical matter and depends on the particular circumstances and disciplines, such as (always-provisional) scientific confirmation at some scale of appearance/fidelity.
Representation and manifestation are often intertwined with interpretation.
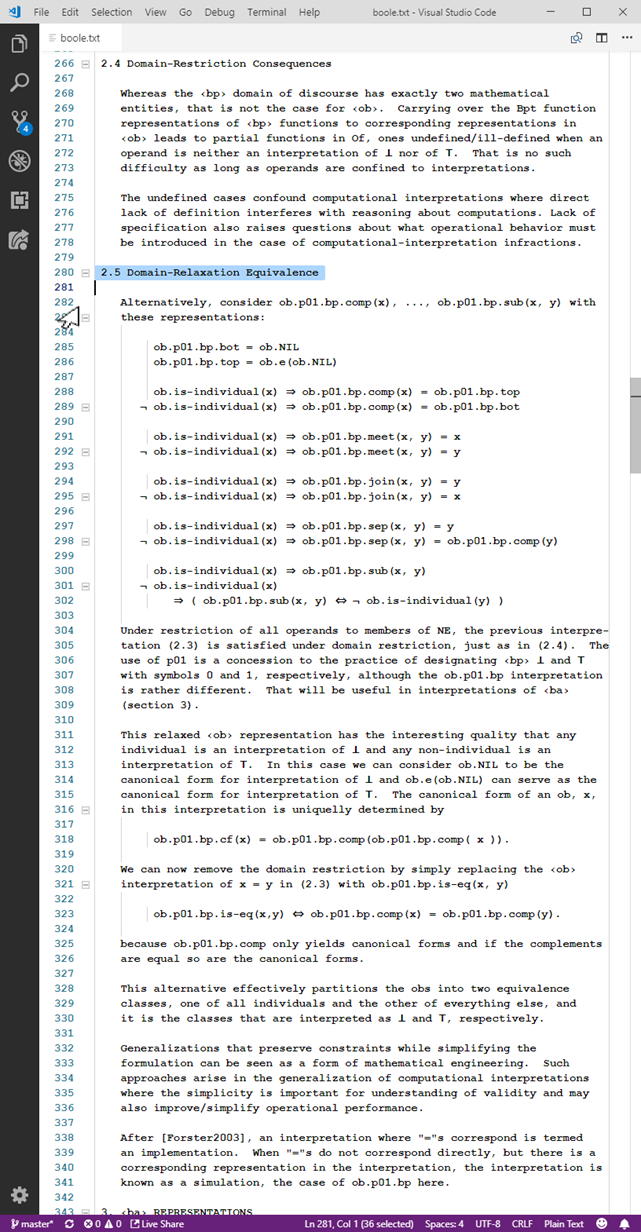
4. Concerning Representational Equivalence Ambiguity
Mathematical representation of functions has been illustrated with examples for ‹ob› and also for functions that serve as the interpretation-in-‹ob› of functions in other structures, such as those prefixed ob.p01.bp and ob.bvx. It is generally the case that there are many representations of a single function, based on the principle of extensional equivalence: when f( x ) = g( x ) for all x, f and g as defined represent the same function. In these cases, the equivalence is rather sideways, signifying interpretation as the same entity amidst all the functions of the same structure.
“Representation” is used in one other sense here with respect to conditions on the structure ‹B› in which interpretation of structure ‹A› is established. Representation is akin to establishment of a portion of ‹B› that encompasses the interpretation of ‹A› but without restriction to uniqueness of representatives (although uniqueness is not ruled out). Many entities, the representatives, of the representation of ‹A› in ‹B› may be taken as equivalent interpretations of interpreted as the same entity in ‹A›, including the designated (characteristic or canonical) interpretation of that entity in ‹B›. In this manner Equivalent representatives reflect back to a distinct entity of ‹A› and any of them can be regarded as if interpretations of that entity in ‹B›.
Representation in this manner is not arbitrary; validity of representation hinges on preservation of interpretation validity among all substitutions of equivalent representatives. Valid representations are entirely interpretation preserving.
An intended representation is entirely in ‹B› and, generally, the same entities and ‹B›-represented functions are not excluded from employment in any number of other representations, whether in respect to ‹A› or some other structure.
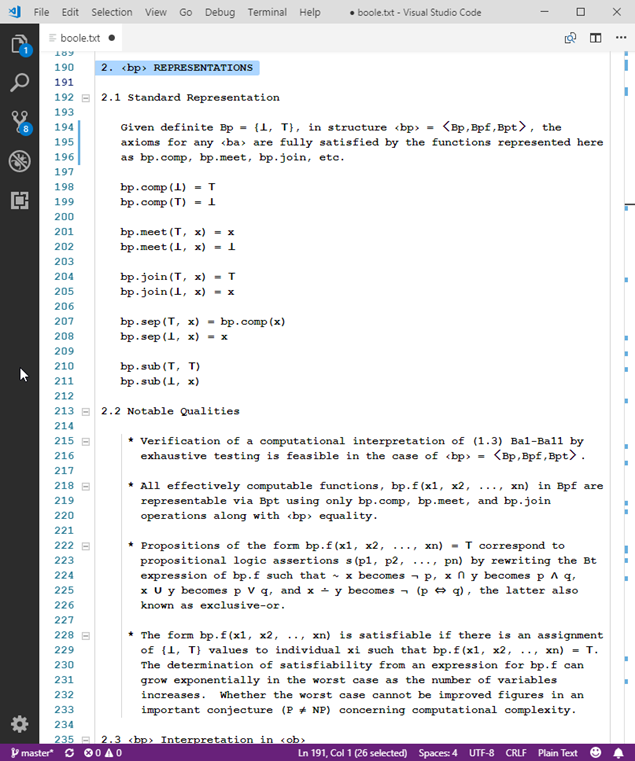
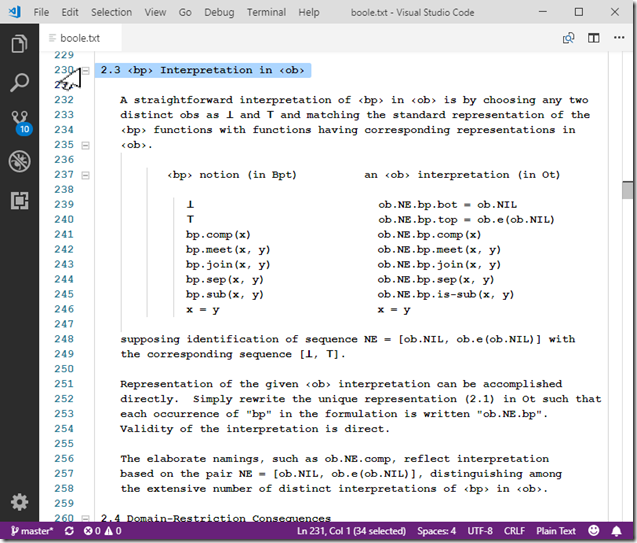
For example, in boole.txt, the (section 2.3) the ob.NE.bp representation of ‹bp› in ‹ob› is strict with respect to interpretation of the ‹bp› domain entities ⊥ and ⊤, along with corresponding function representations of the ‹bp› primitive notions (axiomatic functions). In contrast, the (section 2.5) ob.p01.bp representation preserves the ob.NE.bp interpretation while having every ob represent one of ‹bp› ⊥ and or ⊤. The ob.p01.bp functions corresponding to ‹bp› primitive notions properly simulate ‹bp›. the interpretation. The function ob.p01.bp.comp( x ) and agreement on canonical form are revealing in respect to interpretation ob.NE.bp consistency and interpretation preservation as canonical in of the ob.p01.bp representation.
The boole.txt (section 3.4) representations ob.bvx of ‹ba› demonstrate that the same ob can serve in many representations. It is not intrinsically-apparent which representation (whether ob.po1.bp, ob.bvx, or something else entirely) is intended. When particular canonical forms are observed, it is more suggestive, yet not conclusive. (Nevertheless, gifted accomplished computer-software maintainers are excellent at inference of the purpose of program aspects and identifying consistent repairs for representation breakdowns. That’s based on domain knowledge and the context in which the software is applied as well as not merely cues in the code.)
It is valuable to express derived obs in a form that signifies what they are intended representatives for. what they represent other than merely obs as themselves, in specific situations. Such discrimination of representations and related cases involving tracking of interactive-operation states and ephemeral entities are beyond the ‹ob› model; they’ll be investigated once the “pure” ‹ob› computational model has been explored. For now it is noteworthy that obs themselves do not reveal intended representations and that serves computational representation quite well as a in the computational-model foundation formulation.
5. Choreography of Computation
Computational processes are abstract beings that inhabit computers. …
A computational process … cannot be seen or touched. It is not composed of matter at all. However, it is very real.
— Building Abstractions with Computers, Chapter 1 in
“Structure and Interpretation of Computer Programs,” ed.2
Mathematical structures can be thought of as static: “standing still.” There is a domain of discourse, such as Ob, and (functional) relationships; deductions can remain to be established. Just the same, nothing moves. It is as if it is all there in the first place (whether or not there’s any actual “there” there).
“Computational interpretation” has been insinuated as the movement from the mathematical stability of a structure such as ‹ob› to some mechanical process that is carried out, different than the deductions and qualification as effectively-computable, yet consistent with that computability. Something moves, something processes.
Although computational procedures can be animated in a manner that allows the process’s stages to be observed, that is not so easy in writing about it. And that’s not so great in an elaborate computation with representations far removed from the nature of the (familiar) entities being simulated. We need an useful depiction that somehow suggests the essence of computational processes.
 The depiction of a computational mechanism in operation will be illustrated with a diagrammatic pattern, whether animated or not. The rotating gear and flash of power is a pattern for depicting computational performance put into
The depiction of a computational mechanism in operation will be illustrated with a diagrammatic pattern, whether animated or not. The rotating gear and flash of power is a pattern for depicting computational performance put into operation action. This could be a human performance, although our focus is on digital computers and their computational procedures enacted with them.
 Consider that the performing machine operates on some (relatively) tangible form of input to be processed, yielding production of an output result that depends on nothing else than the input and the performance of the machine. Here the I, M, and O signify the particular input format, mechanism, and output format. The subscripted ein and eout refer to specific instances of an encoded input
Consider that the performing machine operates on some (relatively) tangible form of input to be processed, yielding production of an output result that depends on nothing else than the input and the performance of the machine. Here the I, M, and O signify the particular input format, mechanism, and output format. The subscripted ein and eout refer to specific instances of an encoded input encoding and an encoded output encoding.
 It is valuable in this diagrammatic approach to have input and output formats
It is valuable in this diagrammatic approach to have input and output formats need to couple properly with the nature of the computing mechanism and its performance. Conformance of the input-output formats with provisions of the mechanism are signified by sockets that couple the input-output with the respective aspects of the mechanism symbol. In this simple input-processing-output diagramming, it is a condition that the specification of the mechanical-operation process have the input and output characterized in the same terms — levels of abstraction — as and the input and output formats are be described in the same terms – a consistent level of abstraction.
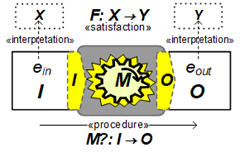 The idea of encoding is critical in grasping what the computation amounts to and also how we consider the use of the computation by representing (encoding) entities of interest.
The idea of encoding is critical in grasping what the computation amounts to and also how we consider the use of the computation by representing (encoding) entities of interest.
At the level of the device, M, the M?:I→O symbolism is short-hand for the function by which every input, ein has a determined output eout in accordance with an assumed procedure’s performance at that level. This is itself likely to be an abstraction above the physical mechanism, whatever its form. The M?:I→O procedure has a description to which the machine’s operation exhibits fidelity in the sense that procedure’s conclusion predicts the output of the machine for a given input. Although the description of the procedure is static, this diagram signifies it being carried out mechanically.
In making use of the device/computation, above, there is also potentially a superior level of abstraction. Consider interpretation of taking some ein as representations of values, x, of some kind X, with interpretation of the derived eout as representing values, y, of kind Y. With respect to those interpretations representations, the input and the derived output are taken as satisfying the functional relationship symbolized as F:X→Y. That is, the procedure enacted by the device is reliable for satisfaction of that functional relationship between its input and its output. The ein qualifies as a representation of a chosen x. The diagrams feature interpretation over representation, and draw the arrows as interpretations from the representations because it is the interpretation that is considered the intention for selection of a (representative) encoding.
To operate computations on the pattern above, an user must select a machine that provides a suitable M and its M?:I→O operation, then derive inputs that represent chosen members of X in order to achieve an output that is representative of the correct result in Y.
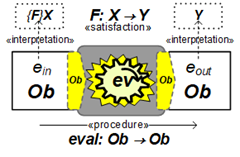 If M is programmable in some manner, there is more variety of choice for intended usage. For example, computational interpretation of obap.eval( e ) allows representation of expressions that can be considered to express F and X together in satisfying F:X→Y with the computed output.
If M is programmable in some manner, there is more variety of choice for intended usage. For example, computational interpretation of obap.eval( e ) allows representation of expressions that can be considered to express F and X together in satisfying F:X→Y with the computed output.
In this example the computational process, so construed, is that of an ob calculator.
In this particular example, we have hand-waved the existence of a mechanical procedure that, when completed on valid input ein, yields an ob (representation) that satisfies
eout = obap.eval (ein )
At this level, we are indifferent to how that is accomplished via the mechanical procedure, simply relying on the fact that it is. What are fixed for this purpose are an ontological commitment to the procedure manifesting obap.eval, so that we can then rely on the representation and satisfaction of F:X→Y. Consider that we are granting existence to both levels and assuming validity of the connection between them reflected in the interpretations. This act rules out other interpretations in the context of the depicted computation.
Variations on this pattern arise as Miser Project conceptualization progresses. The key feature is distinguishing what a computation is (such as the eval procedure and the chosen input) versus what a computation is for (purposive use) and how that figures in representation validity and powerful layering of abstractions/representations. The gaps between what the computations are versus what they are used for will increase along with greater utility, usability and invisibility of the machinery.
This painstaking diagrammatic depiction of an algorithmic computational process establishes the essential ideas of the connection between mechanical procedures and the computational interpretation of mathematical structures. It will be extended for streamlined use in the coordination of multiple computational processes. Establishment of the mechanical procedures and their faithful engineering will also be addressed.
6. Manifestation and Tacit Awareness
There is a point with computers where the experience of using the computer is recognized as manifestation of something that is evoked by the exhibition of computational-processing activity.
 It is easier to see how we manifest something in looking at something rather static, such as words on a page. In reading, the automatic tendency is to discern a sense of the text without much examination word-by-word, unless this is not your language or there are other circumstances that bring attention to the individual words.
It is easier to see how we manifest something in looking at something rather static, such as words on a page. In reading, the automatic tendency is to discern a sense of the text without much examination word-by-word, unless this is not your language or there are other circumstances that bring attention to the individual words.
 That is different than looking at individual words in isolation and then the individual letters and then the marks on which the letters are built.
That is different than looking at individual words in isolation and then the individual letters and then the marks on which the letters are built.
Consider that when we focus on the sense that occurs to us, that is the object of focal attention/awareness. Subordinate attention/awareness is on observation of the substrate, the individual words and perhaps the sense of those in isolation.
 When the sense is stripped away completely, at a level so subordinate that there is no
When the sense is stripped away completely, at a level so subordinate that there is no suggested sense tacit recognition (as in the enlarged tip of an electronic a visual rendition of “w”), we can discern how at the level of the electronic device’s operation, the manifestation of letters, words, and sentences – statements – is achieved by something entirely subordinate. In this case, the manifestation has been engineered by organization of such that miniscule electronically-generated features to manifest are organized to present the text that is in-turn evocative of is chosen to carry a communication.
When text is in your natural language and you are practiced at reading it, there is difficulty in not it takes effort to avoid automatically grasping some sense of the text. It is easy to conclude that behave as if meaning is found on the page, separate from us. Effort is required to strip away the focal and bring awareness to the subordinate; the tacit reaction is reading the text, even for a single word. It is valuable, in for understanding how computers are so marvelous, to appreciate who is making that leap and how affordance of that is engineered.
Having examined the three images, above, and understanding the text here, how automatic is it to identify the third, fragmentary image, as “W”?” Put another way, don’t think of “W” there. It could, after all, be a fragment of “Y” or “X”. It could also depict a section of a girder, of a strut, or of some other material object.
Finally, suppose, instead, that the text images above were replaced with Japanese calligraphy and how difficult it would be for a Japanese-illiterate reader to recognize anything but unintelligible markings at all levels of magnification. An odd case could be made with Egyptian hieroglyphics where there are recognizable figures yet without tacit meaning as communications available to most of us.
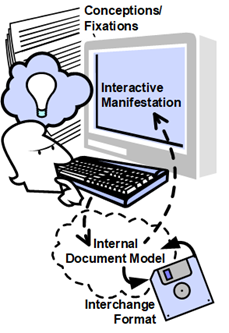 Tacit recognition is important in how manifestations are evoked with so much fidelity that the manifest
Tacit recognition is important in how manifestations are evoked with so much fidelity that the manifestation entity is perceived as being manipulated and preserved by computer interaction. The accomplishment is a wonder of engineering of engineered subordinate processes to achieve such fidelity without interference (except when it doesn’t). This applies in almost every use of electronic digital devices, whether for audio or video, text, or images. Its origin goes back to telegraphy and before that, printing, and before that, writing, and before that, maybe cave paintings and, of course, speech.
In the example of electronic documents and modern word-processing software, the levels of representation and interpretation that are navigated are typical. The interactive manifestation is unrecognizable in the isolated file format that is used for saving and interchanging a representation of the document, successful manifestation depending entirely on the interoperable availability of computer software on different computers. Computer software enacts some form of internal document model by which the interchange format and the manipulatable manifestation are coordinated. The process does not intrude on perception of the manifest document and the author/user perception of the conceptual document and how it might appear in print or some other fixed medium.
Even simplified word-processing models are beyond the immediate reach of the ‹ob› model of computation. There will be appeals and demonstrations of manifestation, starting at lower levels of computer operation before higher-level ones are considered. The idea is to use such simplifications to gain a grasp on what is happening underneath the marvelous practical computers available to us.
One case of tacit (mis-)understanding will arise early. It is easy, for computer programmers and others, to recognize a formula that has some mathematical appearance as expression of a computation; this mistaken attribution of mathematics as being about computation is encouraged by the borrowing of mathematical notation for programming-language purposes. Since ‹ob› and the associated model of computation are unfamiliar in a programming context, that confusion is avoidable for a time. With familiarity using the Miser Project coding notation (oFrugal) for computation of obs, tacit understanding will likely kick in and we’ll need to keep that harmless.
7. Ontological Commitment: Layered Abstractions
The elevator of ontological commitment does not stop between floors.
— anon. The Wit and Wisdom of Twitter.
In considering the ways that computers are employed to manifest layers of abstract entities, and interpretations of other entities in those, it is useful to identify and assert ontological commitments.
In use of “manifestation” with respect to interactions with a computer, it is important to distinguish the (subordinate) form that is exhibited to us from the (theoretical) entity that is taken to be (focally) manifest. The degree to which we can successfully behave as if the theoretical entities are somehow present, as “there,” involves an ontological commitment on our part; we grant being to the (theoretical) entities and fidelity to the manifestations. The engineering of computer systems and their software is successful to the degree that orchestration of intended manifestation supports such commitment without confusion.
Consider that particular representations (in ‹ob› or of ‹ob›, or in other structures) might become so familiar that a tacit interpretation is manifest immediately. This can be a case of tacit ontological commitment, whether warranted or not.
An useful variety of ontological commitment is with the diagrammatical illustration of an obap.eval algorithm carried out by a computational mechanism (section 5, above). One can trust in the achievement of an obap.eval algorithm and fix that level for faithful representation in service of a higher level of abstraction. In this sense, there can be focus on the two levels without regard for potential different ones, intermediary levels, and especially subordinate ones. The fidelity of the lower-level manifestation of ‹ob› is a premise in the valid representation of the higher level.
The danger of misguided ontological commitment is with regard to category mistakes. A common example is the confusion of computational representations with objects in our reality (such as persons, other animate entities, and organizations of such entities).
Exploring the Miser Project model can seem far removed from questions of the social benefit and purposive use of computers and problems of inappropriate ontological commitments. There will be simple cases that provide miniature demonstration of such hazards. Mainly, there will be tolerance of benign ontological commitment, especially the fixing of levels of abstraction and the representation of one in the other.
Onward to the oMiser computational model.

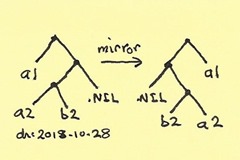 mirror( t1 )
mirror( t1 )